Dadas dos matrices del mismo orden, A y B, se define su suma como otra matriz, C, del mismo
orden que las matrices sumando cuyos elementos se obtienen sumando a cada elemento de la primera
matriz, A, el correspondiente elemento de la segunda matriz sumando, B:
Resta
La resta de dos matrices del mismo orden A y B, se define como la suma de A más la matriz
opuesta de B, por lo que resultará ser otra matriz del mismo orden, D, cuyos elementos se obtienen de
restar a cada elemento de la primera matriz A (minuendo) el elemento correspondiente de la matriz que
resta, B (sustraendo).
Producto de una matriz por un número.
Dada una matriz A = [ aᵢⱼ]ₘₓₙ y número real α∈R, se define el producto de un número por esa
matriz como otra matriz B del mismo orden cuyos elementos se obtienen de multiplicar cada uno de
los elementos de A por el número α:
Producto de matrices.
Para poder multiplicar dos matrices A y B, ( A ⋅ B), el número de columnas de la matriz que
multiplica en primer lugar, A, debe ser igual al número de filas de la matriz que multiplica en segundo lugar, B. Así pues, dadas dos matrices Aₘₓₙ, Bₙₓₚ, el resultado de multiplicar A por B, A ⋅ B, es otra matriz C = A ⋅ B, con tantas filas como la matriz que multiplica en primer lugar y tantas columnas como la matriz que aparece en el producto en segundo lugar, Cₘₓₚ. Los elementos de la matriz C se obtienen de multiplicar las filas de la primera matriz por las columnas de la segunda matriz. Ese producto consiste en multiplicar un elemento de la fila por el correspondiente de la columna y sumar el resultado al resto de productos de elementos de esa fila por esa columna.

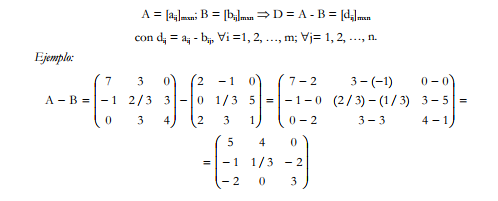




No hay comentarios:
Publicar un comentario